El sonido digital está presente en nuestra vida diaria, pero pocas veces nos detenemos a entender cómo una vibración del aire se transforma en datos que un ordenador puede procesar. Este artículo es el primero de una serie dedicada al procesamiento de señales de audio con Python, en la que exploraremos de forma progresiva los fundamentos del audio digital combinando teoría clara y ejemplos prácticos. Comenzaremos por la onda seno y por conceptos esenciales como frecuencia, amplitud y fase, acompañados, como no podía ser de otras manera, de la correspondiente implementación en Python con la que generaremos y graficaremos, nuestras primeras señales de audio.
La onda seno como componente fundamental del sonido.
Desde el punto de vista matemático y físico, una onda seno (también llamada senoidal o sinusoide) representa el caso más simple de señal periódica. Es especialmente importante porque cualquier señal sonora compleja (que generaremos en futuros artículos) puede descomponerse en una suma de ondas seno de distintas frecuencias, amplitudes y fases, como establece la teoría de Fourier. Por esta razón, la onda seno se considera el “átomo” del sonido en el dominio digital. Esta especial relevancia de la onda seno, justifica que prestemos especial atención a su expresión matemática, que viene dada por la siguiente fórmula:

Esta expresión contiene algunos elementos de especial relevancia, que pasamos a enumerar y explicar brevemente, a continuación:
Frecuencia (): Medida en hercios (Hz), la frecuencia indica el número de ciclos completos que la onda realiza por segundo. Está directamente relacionada con el tono percibido. En el rango audible humano, que va aproximadamente de 20 Hz a 20 kHz, las frecuencias bajas se perciben como sonidos graves y las altas como sonidos agudos. Por ejemplo, una señal de 100 Hz produce un sonido grave, mientras que una de 8000 Hz resulta claramente aguda.

Amplitud (A): Representa la magnitud de la señal y está asociada a la percepción del volumen, aunque esta relación no es lineal debido a las características del oído humano. A menudo, en audio digital, las señales suelen normalizarse en el rango [−1,1] para facilitar el procesamiento y evitar distorsión por saturación.

Fase (φ): Describe la posición de la onda dentro de su ciclo en un instante dado. Aunque no se percibe directamente como un atributo aislado, la fase es crítica en fenómenos como interferencias, cancelaciones, alineación temporal y procesamiento estéreo. Dos señales con la misma frecuencia y amplitud pueden sumarse o cancelarse parcialmente dependiendo de su fase relativa.

El sample rate y la representación temporal del sonido.
En este punto, es procedente hacer alusión al concepto de frecuencia de muestreo (o sample rate). Esta magnitud define cuántas muestras por segundo se toman para representar una señal de audio de forma digital. En la práctica, determina la resolución temporal de la señal y establece la frecuencia máxima que puede representarse sin aliasing, según el teorema de Nyquist (del que hablaremos en un futuro artículo de esta serie).
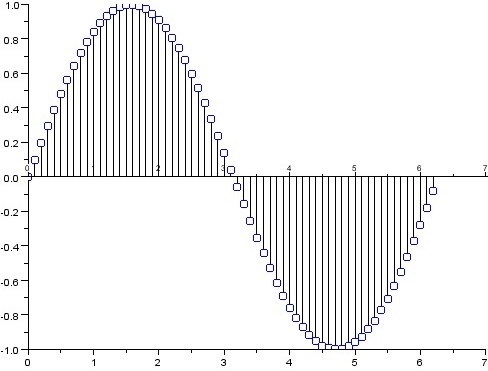
Implementación en Python.
Visto un poco de teoría, pasaremos a continuación a la práctica, mostrando un sencillo script en Python, en el que generaremos, graficaremos y guardaremos en un archivo WAV, nuestra primera señal de audio, especificando la frecuencia, la amplitud y la duración (que multiplicado por el sample rate nos dará el parámetro tiempo (t) de nuestra fórmula). De este modo, empezaremos importando las librerías que vamos a emplear. Para a continuación, definir el valor de las variables fundamentales de la onda seno:

Como se ve, para el sample rate (variable sr) hemos usado un valor de 44100 Hz que es el estándar del audio digital, lo que significa que la señal se evalúa 44100 veces por segundo. Este valor lo utilizaremos para construir el vector de tiempo (t) y asegurar que la onda seno tenga una representación precisa, además de garantizar que el archivo WAV generado sea compatible con la mayoría de sistemas y reproductores de audio. En este caso, a las variables relativas a la frecuencia y la amplitud, les asignaremos valores de 440 y 0.5 respectivamente. Dado que, para este ejercicio la variable fase no es relevante, la dejaremos en 0.
Definidas las variables fundamentales, el siguiente paso será definir el vector de tiempo para nuestra señal. Para ello utilizaremos el método linspace() de numpy:

Con ello, generaremos un vector de tiempo que representa cada instante en el que se tomará una muestra de la señal de audio, desde 0 hasta la duración total. El número de puntos se calculará multiplicando la frecuencia de muestreo por la duración, lo que asegura una muestra por cada intervalo temporal correspondiente al sample rate. Finalmente, el uso de endpoint=False evita incluir el instante final y previene errores de muestreo o discontinuidades en la señal.
Una vez definido el vector de tiempo, ya tenemos todos los valores necesarios para construir nuestra onda seno a partir de la expresión matemática que vimos al principio. Tras ello, mostraremos por pantalla el contenido de nuestra señal, aunque limitándonos a los 100 primeros valores de la misma:


Como se ve en la salida, la señal generada se compone de una serie de valores discretos, que la hacen apta para ser procesada digitalmente. También notamos que dichos valores se encuentran comprendidos entre -0.5 y 0.5. Lo cual viene dado por el valor de 0.5 que escogimos para la amplitud de la señal.
A continuación, procederemos a usar la librería matplotlib para mostrar gráficamente la señal, a partir de las 1000 primeras muestras:


Con ello, ya tendríamos generada y representada nuestra primera señal digital. Para ver que tal suena, procederemos a utilizar scipy.io y su módulo wavfile para generar el correspondiente archivo de audio:

Como se ve, en este bloque de código convertimos la señal de audio, que está representada en valores de punto flotante entre −0.5 y 0.5, al formato entero de 16 bits requerido por los archivos WAV estándar. Al multiplicar la señal por 32767 se escala para ocupar todo el rango dinámico disponible sin saturar, y la conversión a int16 transforma los datos en un formato compatible con audio PCM. Finalmente, la función wavfile.write guarda la señal en un archivo WAV, utilizando la frecuencia de muestreo indicada para que el sonido se reproduzca correctamente.
CONCLUSIÓN.
Este primer artículo ha establecido las bases necesarias para entender cómo se representa y genera el sonido en el dominio digital usando Python. En el próximo artículo de la serie profundizaremos en el proceso de muestreo, el teorema de Nyquist y el fenómeno del aliasing, explorando qué ocurre cuando una señal no se muestrea correctamente y cómo estos efectos pueden observarse y escucharse mediante ejemplos prácticos y visualizaciones.
Saludos.

