Procesamiento de señales de audio con Python (Parte 2): Muestreo y aliasing

Saludos y bienvenidos a este segundo articulo de la serie Procesamiento de señales de audio con Python. En el artículo anterior sentamos las bases del sonido digital generando una onda seno y convirtiéndola en un archivo de audio. En esta segunda parte vamos a dar un paso clave: entender qué ocurre cuando una señal continua se muestrea, qué límites tiene ese proceso y por qué una mala elección del sample rate puede introducir errores audibles. El objetivo de este artículo es experimentar directamente con Python para escuchar, ver y provocar el aliasing, uno de los fenómenos más importantes del audio digital.

TECNICA DE MUESTREO Y EL TEOREMA DE NYQUIST.

El muestreo es el proceso fundamental que permite convertir una señal analógica, continua en el tiempo, en una señal digital formada por valores discretos que un ordenador puede almacenar y procesar. La frecuencia de muestreo (sample rate) determina cada cuánto tiempo se toma una “fotografía” de la señal original y, por tanto, define el nivel de detalle con el que esa señal será representada. Un sample rate demasiado bajo provoca pérdidas de información y distorsiones irreversibles, mientras que uno adecuado permite capturar fielmente el contenido espectral de la señal. Aquí es donde entra en juego el teorema de Nyquist (o de Nyquist – Shannon), que establece que la frecuencia de muestreo debe ser al menos el doble de la frecuencia más alta presente en la señal para evitar el aliasing, garantizando así una digitalización correcta y sin ambigüedades. Podemos plasmar dicho teorema en la siguiente expresión:

Aquí, la frecuencia $f_s / 2$ se conoce como frecuencia de Nyquist. Donde cualquier componente espectral por encima de este límite no podrá representarse correctamente y dará lugar a distorsión (aliasing). Para ilustrar esta idea de un modo practico, recurriremos al siguiente programa en el que, establecido un sample rate relativamente bajo (8000 Hz), generaremos varias audios (mucho cuidado al reproducirlos, sobre todo si usan auriculares) con frecuencias cuyos valores se encontrarán tanto por debajo como por encima de Nyquist, para finalmente mostrar la grafica correspondiente a la frecuencia generada de modo incorrecto (con aliasing). Apuntar también que, dado que estamos experimentando con señales simples, la frecuencia máxima coincidirá con la asignada al principio, al ser constantes en nuestros ejemplos:

Pasemos, a continuación, a ejecutar el script:

Como se puede comprobar, la salida del programa nos muestra el valor de Nyquist que constituye la frecuencia máxima que puede ser correctamente generada y representada con un sample rate, en este caso, de 8000 Hz (ya que 8000 / 2 = 4000) de modo que de los audios generados a continuación, solo el último de ellos (con frecuencia de 45000Hz, que es superior al valor de Nyquist) se generará con aliasing. Esto no supondrá un fallo en el programa, simplemente que el tono generado no se corresponderá al que debería generarse con esa frecuencia (el sonido generado aparecerá claramente distorsionado). Esta falta de correspondencia puede verse también graficando esta última señal (cosa que hace el código a continuación):

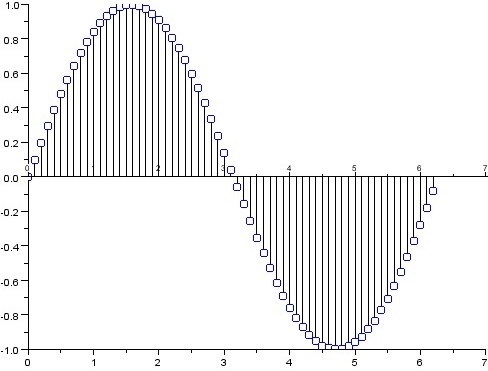
En la gráfica de una señal aliasada la forma de onda deja de parecer una senoide suave y regular, y aparece distorsionada, con oscilaciones más lentas de lo esperado. Aunque el tono original era de alta frecuencia, la señal muestreada parece corresponder a una frecuencia más baja, como si la onda se “plegara” sobre sí misma. Este efecto visual refleja exactamente el aliasing: el sistema digital interpreta erróneamente una frecuencia por encima de Nyquist como otra distinta dentro del rango permitido, produciendo una señal que no coincide ni en forma ni en contenido con la original.

ELIGIENDO FRECUENCIA DE MUESTREO ADECUADA.

A partir de este punto, cabe preguntarse por cual ha de ser el sample rate a emplear para que la totalidad de las señales se genere de manera adecuada. Esto lo haremos con la operación inversa a la empleada para calcular el valor de Nyquist:

Por lo que el sample rate, mínimo a usar en nuestro caso sería de 9000 Hz (ya que 2 * 4500 = 9000). Sin embargo, aunque el valor de 9000 Hz, aquí, cumpliría teóricamente el teorema de Nyquist para un tono de 4500 Hz, al situarse exactamente en el límite mínimo, no deja margen de seguridad y produce una representación muy pobre de la señal, con solo dos muestras por ciclo (haciendo que el audio generado sea casi imperceptible como sería en este caso). Y es que, en la práctica, las señales reales no son senoides ideales (como los que hemos estado viendo hasta ahora) y contienen armónicos, transitorios y ruido (no se preocupen, dentro de poco empezaremos a experimentar con señales compuestas), además de que los filtros antialiasing no son perfectos, por lo que trabajar al límite aumenta el riesgo de distorsión. Por esta razón, en audio se emplean frecuencias de muestreo estándar como 44.1 kHz o 48 kHz, que proporcionan suficiente margen para capturar correctamente todo el contenido espectral audible y garantizar compatibilidad, estabilidad y calidad en los sistemas de grabación y reproducción. Ejecutemos nuevamente nuestro programa, pero ahora, usando un sample rate estandard de 44100 Hz (44.1kHz):

Vemos como la situación cambia ostensiblemente al ver como el valor de Nyquist, ahora es de 22050 Hz. Lo que cubre con creces el valor de todas las frecuencias que queremos representar. Incluida la de 4500 Hz, que ahora, presentará la siguiente gráfica sin distorsiones:

CONCLUSIÓN.

En este capítulo hemos visto cómo el proceso de muestreo y la elección del sample rate condicionan de forma directa la fidelidad de una señal digital, comprobando de manera práctica qué ocurre cuando se viola el teorema de Nyquist y cómo aparece el aliasing. Hemos trabajado en el dominio del tiempo, escuchando y visualizando las señales para entender sus limitaciones. En el próximo capítulo daremos un paso más y cambiaremos de perspectiva: entraremos en el dominio de la frecuencia, trabajaremos con señales compuestas, aprenderemos a descomponer estas mediante la Transformada de Fourier (FFT) y veremos cómo analizar y visualizar su contenido espectral para comprender con mayor profundidad qué está ocurriendo realmente dentro del audio.

Saludos.

Concurrencia y paralelismo en Python usando hilos y procesos con ‘concurrent.futures’.

Hace algún tiempo estuvimos hablando de la programación concurrente en Python. En aquel articulo vimos como la concurrencia es una técnica fundamental en programación que permite ejecutar varias tareas de forma simultánea o solapada, mejorando el rendimiento y la capacidad de respuesta de las aplicaciones. Pues bien, en el artículo de hoy, hablaremos un poco de concurrent.futures, el cual, constituye un módulo de la biblioteca estándar de Python (por lo que no se requiere de ninguna instalación adicional) que nos permitirá ejecutar tareas de manera concurrente de un modo sencillo. Además nos permitirá trabajar tanto con hilos (threads) como con procesos facilitando la paralelización de tareas y sin tener que gestionar manualmente los detalles de bajo nivel de la concurrencia.

Esquema básico del enfoque de programación concurrente.

Esquema básico del enfoque de programación paralela.

Este módulo se basa en el concepto de ejecutores (executors), que son objetos responsables de administrar un grupo de hilos o procesos y ejecutar funciones de manera asíncrona. Los dos ejecutores principales son ThreadPoolExecutor, orientado a tareas de entrada/salida, y ProcessPoolExecutor, más adecuado par tareas que requieren un uso intensivo de la CPU.

DESCARGA CONCURRENTE DE PÁGINAS WEB CON ThreadPoolExecutor.

En primer lugar, ThreadPoolExecutor es especialmente útil cuando se trabaja con operaciones que pasan mucho tiempo esperando, como solicitudes de red o acceso a archivos. Un caso típico puede ser, por ejemplo, la descarga de varias páginas web utilizando hilos, permitiendo reducir el tiempo total de ejecución:

En este código, submit() envía cada tarea al ejecutor y devuelve un objeto Future. Por su parte, el método as_completed() permite procesar los resultados a medida que cada descarga finaliza, sin esperar a que terminen todas. Esto mejora significativamente el tiempo total de ejecución frente a una versión secuencial.

OUTPUT:

USO INTENSIVO DE CPU CON ProcessPoolExecutor.

Port otra parte, cuando las tareas requieren mucho cálculo, como operaciones matemáticas complejas, el uso de hilos puede no ser eficiente debido al Global Interpreter Lock (GIL) de Python. Para estos casos, ProcessPoolExecutor permite distribuir el trabajo entre varios procesos, aprovechando mejor los núcleos del procesador. En el siguiente ejemplo abordaremos un caso típico en el que puede ser útil este enfoque como es la adición de valores muy grandes:

En este caso, utilizamos ProcessPoolExecutor para ejecutar en paralelo una tarea intensiva de CPU, concretamente el cálculo de la suma de una secuencia de números grandes. Para ello definimos primero la función suma_grande(), que realiza el cálculo mediante un bucle acumulativo. A continuación, dentro del bloque if __name__ == «__main__», creamos una lista de valores que después enviaremos, cada uno, como tarea independiente a un conjunto de procesos mediante executor.submit(). Cada proceso ejecuta la función de forma autónoma devolviendo el resultado a través de un objeto Future. Por su parte, el bucle as_completed() permite recoger los resultados a medida que los procesos finalizan, mostrando la suma calculada para cada valor. Finalmente, como en el caso anterior, usaremos time.time() para medir el tiempo total de ejecución del conjunto de cálculos.

OUTPUT:

En esta salida queda bien ilustrada la idea de que as_completed() nos permite tomar los resultados a medida que se van completando, en el hecho de que el resultado para 20000000 se muestra el último (lo cual se entiende al ser el mas grande y requerir más tiempo), a pesar de figurar el primero en la lista valores. A diferencia del resultado que obtendríamos con un enfoque secuencial el cual, además, consumiría más tiempo:

Salida utilizando enfoque secuencial.

UTILIZANDO executor.map().

El método map() resulta muy útil cuando se desea aplicar una función a una lista de elementos (como vimos en el caso anterior) y obtener los resultados en el mismo orden. Veamos, así, otro ejemplo en el que nos proponemos convertir una lista de temperaturas de grados Celsius a Fahrenheit:

De este modo, obtenemos un código más compacto que el que tendríamos usando submit() no siendo necesario manejar explícitamente objetos Future, mejorando la legibilidad cuando las tareas son simples.

OUTPUT:

MANEJANDO EXCEPCIONES EN TAREAS CONCURRENTES.

Un aspecto capital a tener en cuenta en aplicaciones que usan la concurrencia es el relativo al manejo de excepciones. Veamos un sencillo ejemplo en el que procesamos una lista de divisiones donde algunas operaciones pueden generar errores, como la división por cero:

En este código, el manejo de excepciones es fundamental para garantizar que un error en una tarea concurrente no interrumpa la ejecución del resto. Cada división se ejecuta en un hilo independiente y, si ocurre una excepción (como la división por cero), esta no se produce inmediatamente, sino que queda almacenada en el objeto Future. Al llamar a future.result(), la excepción se propaga y puede capturarse mediante un bloque try/except. De este modo, el programa puede detectar y reportar errores de forma individual, mientras permite que las demás tareas finalicen con normalidad, logrando un control robusto y seguro de fallos.

OUTPUT:

CONCLUSION.

En conclusión, el módulo concurrent.futures ofrece una forma clara y eficaz de implementar concurrencia y paralelismo en Python, permitiendo ejecutar múltiples tareas de manera simultánea sin complejidad excesiva. Su capacidad para gestionar resultados y excepciones a través de objetos Future facilita la creación de programas más robustos, ya que los errores pueden tratarse de forma individual sin afectar al resto de la ejecución. Al elegir correctamente entre ThreadPoolExecutor y ProcessPoolExecutor según el tipo de tarea a ejecutar, es posible mejorar el rendimiento y la escalabilidad de las aplicaciones, manteniendo al mismo tiempo un código legible y fácil de mantener.

Saludos.

Procesamiento de señales de audio con Python (Parte 1): fundamentos del sonido digital

El sonido digital está presente en nuestra vida diaria, pero pocas veces nos detenemos a entender cómo una vibración del aire se transforma en datos que un ordenador puede procesar. Este artículo es el primero de una serie dedicada al procesamiento de señales de audio con Python, en la que exploraremos de forma progresiva los fundamentos del audio digital combinando teoría clara y ejemplos prácticos. Comenzaremos por la onda seno y por conceptos esenciales como frecuencia, amplitud y fase, acompañados, como no podía ser de otras manera, de la correspondiente implementación en Python con la que generaremos y graficaremos, nuestras primeras señales de audio.

La onda seno como componente fundamental del sonido.

Desde el punto de vista matemático y físico, una onda seno (también llamada senoidal o sinusoide) representa el caso más simple de señal periódica. Es especialmente importante porque cualquier señal sonora compleja (que generaremos en futuros artículos) puede descomponerse en una suma de ondas seno de distintas frecuencias, amplitudes y fases, como establece la teoría de Fourier. Por esta razón, la onda seno se considera el “átomo” del sonido en el dominio digital. Esta especial relevancia de la onda seno, justifica que prestemos especial atención a su expresión matemática, que viene dada por la siguiente fórmula:

Esta expresión contiene algunos elementos de especial relevancia, que pasamos a enumerar y explicar brevemente, a continuación:

Frecuencia ($f$): Medida en hercios (Hz), la frecuencia indica el número de ciclos completos que la onda realiza por segundo. Está directamente relacionada con el tono percibido. En el rango audible humano, que va aproximadamente de 20 Hz a 20 kHz, las frecuencias bajas se perciben como sonidos graves y las altas como sonidos agudos. Por ejemplo, una señal de 100 Hz produce un sonido grave, mientras que una de 8000 Hz resulta claramente aguda.

Amplitud (A): Representa la magnitud de la señal y está asociada a la percepción del volumen, aunque esta relación no es lineal debido a las características del oído humano. A menudo, en audio digital, las señales suelen normalizarse en el rango $[-1, 1]$[−1,1] para facilitar el procesamiento y evitar distorsión por saturación.

Fase (φ): Describe la posición de la onda dentro de su ciclo en un instante dado. Aunque no se percibe directamente como un atributo aislado, la fase es crítica en fenómenos como interferencias, cancelaciones, alineación temporal y procesamiento estéreo. Dos señales con la misma frecuencia y amplitud pueden sumarse o cancelarse parcialmente dependiendo de su fase relativa.

Señal seno con fase 0.

El sample rate y la representación temporal del sonido.

En este punto, es procedente hacer alusión al concepto de frecuencia de muestreo (o sample rate). Esta magnitud define cuántas muestras por segundo se toman para representar una señal de audio de forma digital. En la práctica, determina la resolución temporal de la señal y establece la frecuencia máxima que puede representarse sin aliasing, según el teorema de Nyquist (del que hablaremos en un futuro artículo de esta serie).

Ejemplo de señal muestreada.

Implementación en Python.

Visto un poco de teoría, pasaremos a continuación a la práctica, mostrando un sencillo script en Python, en el que generaremos, graficaremos y guardaremos en un archivo WAV, nuestra primera señal de audio, especificando la frecuencia, la amplitud y la duración (que multiplicado por el sample rate nos dará el parámetro tiempo (t) de nuestra fórmula). De este modo, empezaremos importando las librerías que vamos a emplear. Para a continuación, definir el valor de las variables fundamentales de la onda seno:

Como se ve, para el sample rate (variable sr) hemos usado un valor de 44100 Hz que es el estándar del audio digital, lo que significa que la señal se evalúa 44100 veces por segundo. Este valor lo utilizaremos para construir el vector de tiempo (t) y asegurar que la onda seno tenga una representación precisa, además de garantizar que el archivo WAV generado sea compatible con la mayoría de sistemas y reproductores de audio. En este caso, a las variables relativas a la frecuencia y la amplitud, les asignaremos valores de 440 y 0.5 respectivamente. Dado que, para este ejercicio la variable fase no es relevante, la dejaremos en 0.

Definidas las variables fundamentales, el siguiente paso será definir el vector de tiempo para nuestra señal. Para ello utilizaremos el método linspace() de numpy:

Con ello, generaremos un vector de tiempo que representa cada instante en el que se tomará una muestra de la señal de audio, desde 0 hasta la duración total. El número de puntos se calculará multiplicando la frecuencia de muestreo por la duración, lo que asegura una muestra por cada intervalo temporal correspondiente al sample rate. Finalmente, el uso de endpoint=False evita incluir el instante final y previene errores de muestreo o discontinuidades en la señal.

Una vez definido el vector de tiempo, ya tenemos todos los valores necesarios para construir nuestra onda seno a partir de la expresión matemática que vimos al principio. Tras ello, mostraremos por pantalla el contenido de nuestra señal, aunque limitándonos a los 100 primeros valores de la misma:

Como se ve en la salida, la señal generada se compone de una serie de valores discretos, que la hacen apta para ser procesada digitalmente. También notamos que dichos valores se encuentran comprendidos entre -0.5 y 0.5. Lo cual viene dado por el valor de 0.5 que escogimos para la amplitud de la señal.

A continuación, procederemos a usar la librería matplotlib para mostrar gráficamente la señal, a partir de las 1000 primeras muestras:

Con ello, ya tendríamos generada y representada nuestra primera señal digital. Para ver que tal suena, procederemos a utilizar scipy.io y su módulo wavfile para generar el correspondiente archivo de audio:

Como se ve, en este bloque de código convertimos la señal de audio, que está representada en valores de punto flotante entre −0.5 y 0.5, al formato entero de 16 bits requerido por los archivos WAV estándar. Al multiplicar la señal por 32767 se escala para ocupar todo el rango dinámico disponible sin saturar, y la conversión a int16 transforma los datos en un formato compatible con audio PCM. Finalmente, la función wavfile.write guarda la señal en un archivo WAV, utilizando la frecuencia de muestreo indicada para que el sonido se reproduzca correctamente.

CONCLUSIÓN.

Este primer artículo ha establecido las bases necesarias para entender cómo se representa y genera el sonido en el dominio digital usando Python. En el próximo artículo de la serie profundizaremos en el proceso de muestreo, el teorema de Nyquist y el fenómeno del aliasing, explorando qué ocurre cuando una señal no se muestrea correctamente y cómo estos efectos pueden observarse y escucharse mediante ejemplos prácticos y visualizaciones.

Saludos.

Introducción al Módulo ‘datetime’ en Python.

Saludos y bienvenidos a vuestro blog sobre programación en Python. En esta ocasión vamos a hablar del módulo datetime, el cual, constituye una de las herramientas más utilizadas en Python para trabajar con fechas y horas, y que al formar parte de la biblioteca estándar, no requiere instalación adicional. Se trata de un módulo que nos permitirá realizar operaciones tales como obtener la fecha actual, manipular fechas, calcular diferencias de tiempo o dar formato a fechas y horas.

Este módulo nos va a proporcionar una serie de clases que nos va a permitir manejar fechas, horas y combinaciones de ambas de forma sencilla y precisa. Entre las clases más importantes encontramos las siguientes:

1. date: Para el manejo de fechas (año, mes y día).
2. time: Para el manejo de horas (hora, minuto, segundo y microsegundo).
3. datetime: Para combinar fecha y hora.
4. timedelta: Perfecto para calcular diferencias entre fechas y horas.

EJEMPLOS EN PYTHON.

Visto brevemente en que consiste el módulo, pasemos a ver unos sencillos ejemplos en Python. Para ello, lo primero que haremos será importarlo:

O si lo preferimos, podemos realizar la importación especificando las clases que vamos a utilizar:

Una vez hecho esto, podemos empezar usando la clase date para obtener la fecha actual completa o mostrar la información del año, mes y día, por separado:

A su vez, también podemos emplear la clase date para definir una fecha, especificando el año, mes y día. Por su parte, si lo que queremos es definir también la hora, podremos utilizar la clase datetime:

Esta posibilidad de definir fechas, nos permitirá calcular distancias entre fechas de manera sencilla. Por ejemplo, si queremos calcular la distancia en días entre el 1 de octubre de 2025 y el 1 de enero de 2026, podemos hacer lo siguiente:

Lo mismo podremos hacer, con la clase datetime, incorporando información referente a la hora:

En ambos casos Python nos devuelve un objeto timedelta que representa el intervalo entre ambas fechas. Y es que la clase timedelta nos es de gran utilidad para calcular diferencias entre fechas u horas, así como sumar o restar períodos de tiempo (días, horas, minutos, segundos, etc.) a objetos date y datetime. Siendo especialmente útil para calcular plazos, vencimientos, duraciones y comparaciones temporales de forma clara y precisa. Por ejemplo, supongamos que una tarea debe completarse 48 horas y 30 minutos después de iniciarse:

CONCLUSIÓN:

El módulo datetime es una herramienta esencial para cualquier desarrollador en Python. Su flexibilidad y potencia permiten trabajar con fechas y horas de forma eficiente y segura, facilitando tareas cotidianas y cálculos complejos relacionados con el tiempo, lo cual, nos facilitará notablemente el trabajo cuando tengamos que gestionar ese tipo de información.

Saludos.